Conics
| Saturday, 3 September 2022 | |
| 2-minute read | |
| 315 words | |
Conic Sections
- degenerate conics - point, line
- parabola
- circle
- ellipse
- hyperbola
Parabolas
The distance between the focus and vertex is \(p\).
Every point on the parabola is equidistant from the focus to the directrix.
The latus rectum is a constant line that passes through the focus and parallel to the directrix. This line is \(4p\) units long.
\[ (x - h)^2 = 4p(y - k) \]
\[ y - k = \frac{(x - h)^2}{4p} \]
<center>
Remember \(y - k = a(x - h)^2\)
</center>
<center>
Therefore, \(a = \frac{1}{4}p\)
</center>
Circles
\[ (x - h)^2 + (y - k)^2 = r^2 \]
Ellipses
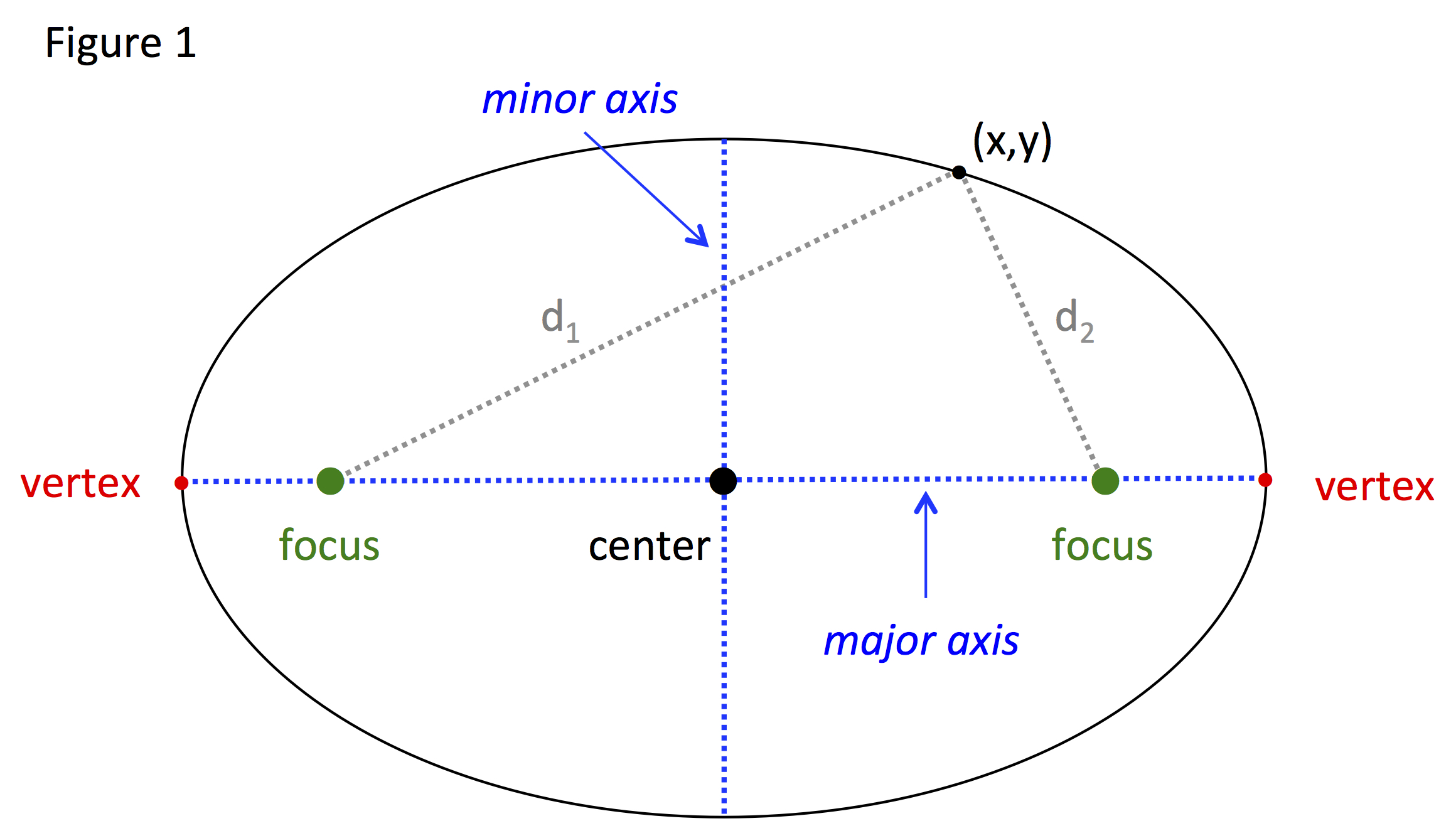
Co-vertices are part of the minor axis and vertices are part of the major axis.
Variables:
\(a\) - the center to a vertex
- \(a\) will always be the longest side
- Known as semi-major axis
\(b\) - the center to a co-vertex
- Known as semi-minor axis
- \(c\) - the center to a focus
- \(e\) - eccentricity describing the dilation of an ellipse
These variables will always form a right triangle, and thus can be written in Pythagorean Theorem.
\[ a^2 = b^2 + c^2 \]
General Formula for Ellipses
Vertical Major Axis
\[ \frac{(x - h)^2}{b^2} + \frac{(y - k)^2}{a^2} = 1 \]
Horizontal Major Axis
\[ \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1 \]
Examples
- Convert the equation into standard form. Then identify center, foci, eccentricity, and endpoints of major and minor axes.
\[ 16x^2 - 96x + 9y^2 + 36y + 36 = 0 \]
Complete the square
\[ 16(x - 3)^2 + 9(y + 2)^2 = 144 \]
Divide both sides by 16
\[ \frac{(x - 3)^2}{9} + \frac{(y + 2)^2}{16} = 1 \]
\(a\) is 16 since \(a\) must be the largest length. Therefore, this is a vertical ellipse.
Center: \((3, -2)\)
Vertices: \((3, -2 \pm 4)\)
Foci: \((3, -2 \pm \sqrt{7})\)